GAN은 Generative Adversarial Nets에서 처음 소개된 아키텍쳐이다. GAN은 딥러닝 기반 생성 모델에 매우 큰 영향을 미쳤으며, 오늘날까지 GAN을 기반으로 한 다양한 파생 모델이 등장하고 있다. 이번 포스팅에서는 GAN에 대하여 간단히 정리해 보았다.
본 포스팅은 다음 자료를 참고하였습니다.
생성 모델(Generative Model)
생성 모델이란 주어진 학습 데이터의 분포를 학습하여 실존하지 않지만 유사한 데이터를 생성하는 모델을 의미한다. 이때 학습 데이터의 분포는 데이터의 종류에 따라 다르게 생각할 수 있다. 가령 학습 데이터가 이미지라면 이미지의 feature, 즉 사람의 이목구비나 이미지의 명도/채도 등에 해당할 것이고, 오디오라면 목소리의 음색이나 높낮이 등에 해당할 것이다. 학습 데이터의 각 feature를 확률 변수로 생각한다면 하나의 학습 데이터는 parameter space에서 하나의 point에 대응될 것이고, 학습 데이터 그룹은 다변수 확률분포를 따를 것이다. 이러한 분포를 모방한 새로운 데이터를 생성하는 것이 생성 모델의 목적이다.
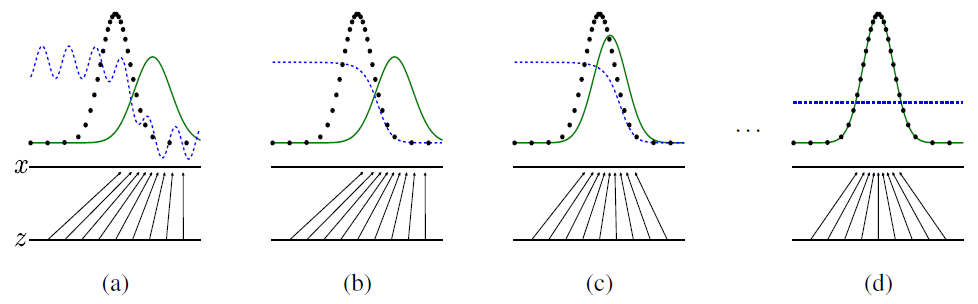출처: 원 논문
적대적 생성 모델(Generative Adversarial Networks, GAN)
GAN은 생성자(generator)와 판별자(discriminator) 2개의 네트워크를 적대적으로 맞서 싸우게 하여 학습하는 모델이다. 흔히 GAN 모델은 경찰과 위조 지폐범의 대결로 비유되곤 한다. 위조 지폐범은 최대한 진짜 지폐와 유사하게끔 위조 지폐를 만들어 경찰을 속일 수 있도록 노력한다. 경찰은 지폐와 위조 지폐를 최대한 구분할 수 있도록 노력한다. 이 둘의 경쟁이 지속되면 위조 지폐범은 진짜와 다름 없는 위조 지폐를 만드는 방향으로 수렴할 것이고, 경찰이 두 지폐를 구분할 수 있는 확률도 1/2로 수렴할 것이다. 이때 위조 지폐범은 generator에, 경찰은 discriminator에 대응된다.
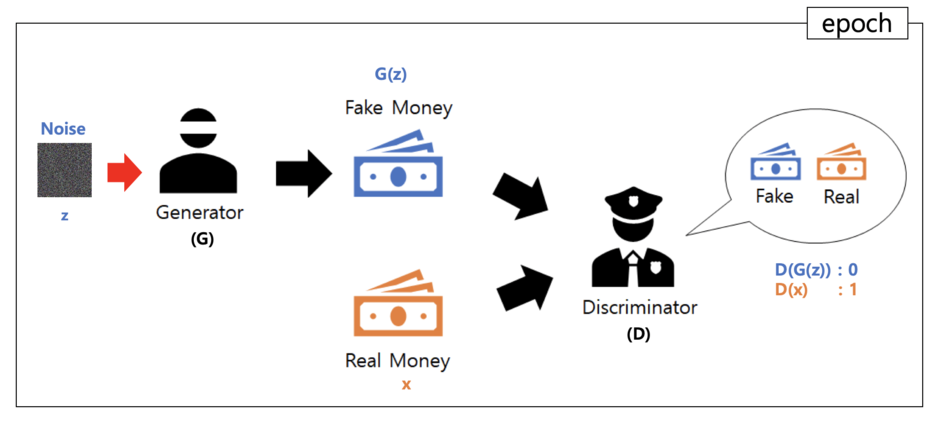위조 지폐범은 최대한 진짜와 가까운 지폐를 만들고, 경찰은 최대한 두 지폐를 구분한다.
임의의 latent vector $z$에 대해 generator $G$는 latent space에서 학습 데이터의 space로 mapping한다고 하자. 또한 discriminator $D$는 데이터를 입력으로 받아 실제 존재하는 데이터에 가까울수록 1을, 존재하지 않는 데이터에 가깝다고 판단되면 0을 출력한다고 하자. 이때 GAN 아키텍쳐는 다음과 같이 구성된다.
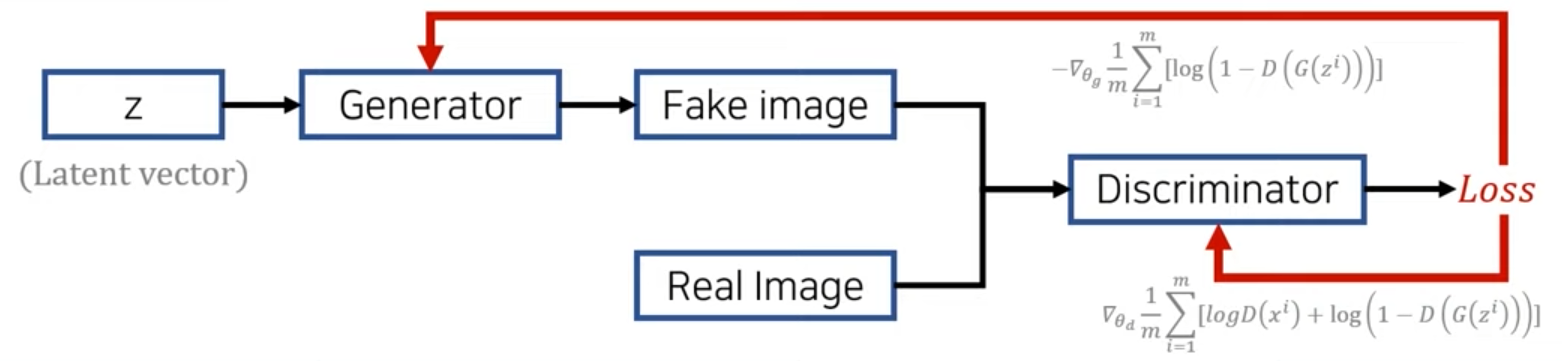출처: GAN: Generative Adversarial Networks (꼼꼼한 딥러닝 논문 리뷰와 코드 실습) 영상 중
$G$는 latent vector $z$로부터 fake data를 생성하여 $D$가 이를 real, 1에 가까운 확률을 출력하도록 학습되어야 할 것이다. 따라서 $G$는 $D(G(z))$가 최대화하는 방향으로 학습되어야 한다. 반대로 $D$는 fake data는 0에 가까운 확률을, real data는 1에 가까운 확률을 출력하도록 학습되어야 할 것이다. 따라서 $D$는 $D(G(z))$를 최소화, $G(x)$를 최대화하는 방향으로 학습되어야 한다. 이 두 사실을 log-loss function으로 묶어 정리하면 다음 수식을 얻는다.
\[\min_{G} \max_{D} V(G, D) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{x \sim p_{z}(z)}[\log(1-D(G(z)))]\]이론적 뒷받침
크게 2가지를 보일 것이다. 첫 번째는 generator $G$가 만드는 확률 분포가 데이터의 확률 분포에 수렴한다는 점이고, 두 번째는 $D(G(z))=1/2$, 다시 말해 $G$가 만드는 fake data와 real data를 $D$가 구분할 수 없는 방향으로 수렴한다는 점이다.
Proposition 1. 주어진 $G$에 대해, 최적 discriminator $D$는 $D_{G}^{*}(x) = \frac {p_{data}(x)} {p_{data}(x) + p_g (x)}$이다.
$Proof.$
\[\begin{align} V(G, D) &= \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_{z}(z)}[\log(1-D(G(z)))] \\ &= \int_{x} p_{data}(x) \log(D(x)) dx + \int_{z} p_{z}(z) \log(1-D(G(z))) dz \\ &=\int_{x} p_{data}(x) \log(D(x)) + p_{g}(x) \log(1-D(x)) dx \end{align}\]연속확률분포의 기댓값 공식에 의해 첫번째 줄에서 두번째 줄로 넘어갈 수 있고, $G$는 latent space를 data space로 mapping하므로 두번째 줄에 치환 적분을 적용하여 세번째 줄로 넘어간다.
이때 함수 $y = a \log y + b \log (1-y)$는 $y = \frac{a}{a+b}$에서 유일한 최댓값을 가진다. 따라서 $D$는 유일한 최적값 $D_{G}^{*}(x) = \frac {p_{data}(x)} {p_{data}(x) + p_g (x)}$이 존재한다.
Theorem 1. $\max_D V(G, D)$는 오직 $p_g=p_{data}$일 때 최솟값을 갖고, 그 값은 $–\log 4$이다.
$proof.$
\[\begin{align} \max_{D} V(G, D) &= \mathbb{E}_{x \sim p_{data}(x)} [\log D^*(x)] + \mathbb{E}_{z \sim p_{z}(z)}[\log(1-D^*(G(z)))]\\ &= \mathbb{E}_{x \sim p_{data}(x)} \left[ \log \frac {p_{data}(x)} {p_{data}(x) + p_g (x)} \right] + \mathbb{E}_{x \sim p_{g}(x)}\left[\log\frac {p_{g}(x)} {p_{data}(x) + p_g (x)}\right]\\ &= \mathbb{E}_{x \sim p_{data}(x)} \left[ \log \frac {2 p_{data}(x)} {p_{data}(x) + p_g (x)} \right] + \mathbb{E}_{x \sim p_{g}(x)}\left[\log\frac {2 p_{g}(x)} {p_{data}(x) + p_g (x)}\right] - \log 4 \\ &= KL\left(p_{data} || \frac{p_{data}(x) + p_g (x)}{2}\right) + KL\left(p_{g} || \frac{p_{data}(x) + p_g (x)}{2}\right) - \log 4 \\ &= 2 JSD(p_{data} || p_{g}) - \log 4 \end{align}\]이때 $KL(p || q)=\int p \log \frac{p}{q}$는 쿨백-라이블러 발산(Kullback–Leibler divergence, KLD)으로, 한쪽에 근사한 확률 분포가 원본과 얼마나 비슷한지 정보 엔트로피 관점으로 측정하는 함수이다. 두 대등한 확률 분포가 얼마나 닮았는지 측정하기 위해 KL-divergence를 symmetric하게 계산한 $JSD(p || q)=\frac{1}{2} \left(KL(p || \frac{p+q}{2}) + KL(q || \frac{p+q}{2}) \right) $ 로 정의하는데, 이를 Jensen-Shannon divergence라고 한다.
$JSD(p || q)$는 $p, q$의 확률분포가 동일할 때 최솟값 0을 가지므로 $\max_{D} V(G, D)$는 오직 $p_g=p_{data}$일 때 최솟값을 갖고, 그 값은 $–\log 4$임이 증명된다. $p_g = p_{data}$일 때 $D_{G}^* = \frac{1}{2}$이므로 $D(G(z)) \rightarrow \frac{1}{2}$로 수렴한다는 사실도 확인할 수 있다.