[LOAM] LOAM: Lidar Odometry and Mapping in Real-time 논문 리뷰

3학년 여름방학동안 김아영 교수님 연구실에서 UROP(Undergraduate Research Opportunity Program) 연구를 수행하였다. 연구 과제는 “4족 보행 로봇 Spot을 위한 HW/SW 시스템 구축”으로, Spot에 탑재할 센서 시스템(LiDAR, IMU, GNSS, Camera) 하드웨어를 설계하고 SLAM 알고리즘을 돌려보는 활동으로 구성되었다. 본 포스팅부터는 여름방학동안 학습한 SLAM 논문을 리뷰하고 Spot으로 실제 측정한 데이터를 바탕으로 SLAM을 돌려보는 과정을 정리해보고자 한다.

Original paper
LOAM: Lidar Odometry and Mapping in Real-time

다음 자료를 참고하였습니다.
LOAM, Lego-LOAM
[SLAM] Lidar Odometry And Mapping (LOAM) 논문 리뷰
SLAM 온라인 스터디 SLAM DUNK 2020 | 정진용님 발표
LeGO-LOAM Line by Line

1. Introduction

LOAM은 논문 제목에서 알 수 있듯이 LiDAR 센서만을 이용하여 odometry와 mapping을 실시간으로 수행하는 SLAM이다. 기존 SLAM 경우 off-line, 즉 데이터 수집 후 프로그램을 돌리는 방식으로 3D mapping을 수행하였고, drift를 보정하기 위해 loop closure를 사용하였다. 그러나 LOAM은 계산 복잡도를 줄여 실시간 SLAM이 가능하도록 하였는데, 이는 전체 알고리즘을 odometry를 계산하는 블록과 mapping 블록으로 나누어 병렬적으로 처리하였기 때문에 가능하였다.

[Note] Terminology

SLAM : Simultaneous Localization and Mapping의 약자이다. 로봇이 주변 환경을 센서로 감지하여 주변 map을 제작하고, map 내에 현재 자신의 위치를 추정하는 작업을 동시에 진행하는 기술이다.

LiDAR : 레이저 센서가 360도 회전(sweep)하면서 주위 환경을 스캔하는 장치이다. 다른 센서와 비교하여 상당한 거리 정밀도를 보이고, 주변 조명과 재질에 둔감하다는 장점이 있다. 센서가 움직이면서 mapping하는 경우 LiDAR의 위치를 계속 추정하는 작업이 필요하다.

Odometry : 로봇이 주행한 궤적을 의미한다. IMU나 wheel encoder를 이용하여 odometry를 추정할 경우 센서 데이터를 계속 적분하게 되므로 시간에 따라 오차가 누적된다. 따라서 궤적이 전체적으로 틀어지는 drift 문제가 발생할 수 있다. 이를 해결하고자 로봇이 이전에 방문했던 위치에 되돌아왔는지 판단하는 loop closure detection을 도입하기도 한다. 본 논문은 loop closure를 포함하지 않고 SLAM 문제를 해결하였다.

2. Notation

Right subcription $k$ : # of Sweeps
$\mathcal{P}_k$ : k번째 sweep으로 얻어진 pointclound 데이터
$\{ L \}$ : LiDAR coordinate system
$\{ W \}$ : World coordinate system
$X_{(k,i)}^{L}$ : LiDAR coordinate system에서 k번째 sweep으로 얻은 i번째 점
$X_{(k,i)}^{W}$ : World coordinate system에서 k번째 sweep으로 얻은 i번째 점

3. System Block Diagram

system_block_diagram 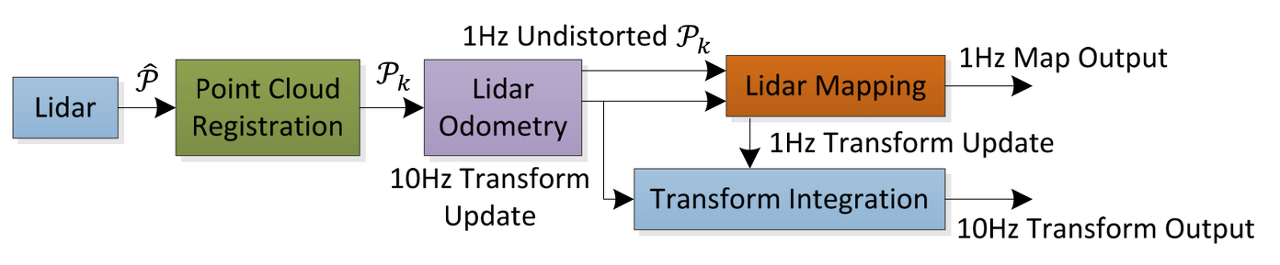출처: 원 논문

LiDAR Odometry : 2개의 연속적인 sweeps을 바탕으로 상대 운동을 계산하는 노드, 10Hz로 수행
LiDAR Mapping : Odometry를 바탕으로 pointcloud를 world coordinate system으로 매칭하는 노드, 1Hz로 수행
Transform Integration : Odometry와 mapping을 바탕으로 현재 로봇의 transform을 계산하는 노드

4. LiDAR Odometry

크게

Feature Point Estimation
Finding Feature Point Correspondence
Motion Estimation

3 단계로 구성된다.

4.1 Feature Point Estimation

$i \in \mathcal{P}_k$인 한 점 $i$에 대해 $i$ 점과 horizontal하게 인접해있는 점들의 집합을 $\mathcal{S}$라고 정의한다. 구현된 코드 상에서는 양쪽 5개씩 총 10개의 점을 사용하였다. 이때 local surface의 curvature $c$를 다음과 같이 나타낼 수 있다.

\[c = \frac{1}{|\mathcal{S}| \cdot \| X_{(k,i)}^{L} \| } \| \sum_{j \in \mathcal{S}, j \neq i} ( X_{(k,i)}^{L} - X_{(k,j)}^{L} ) \|\]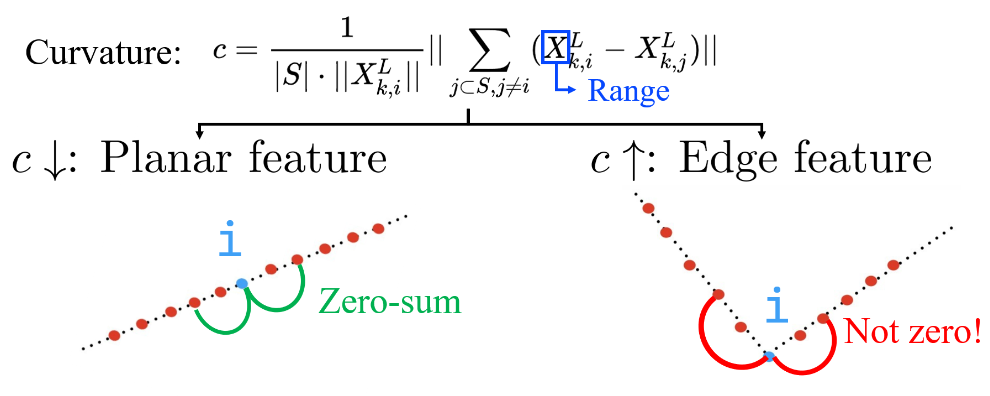

edge_planar_feature 출처: LeGO-LOAM Line by Line - 3. FeatureAssociation (1)

식의 의미를 그림으로 해석해보자. Local surface가 planar한 경우 점들의 depth가 등차수열을 이루므로 $\sum_{j \in \mathcal{S}, j \neq i} ( X_{(k,i)}^{L} - X_{(k,j)}^{L} )$ 값이 양쪽에서 서로 상쇄되어 0에 가까운 값이 나올 것이다. 반면 local surface가 edge와 같이 뾰족할 경우 $\sum_{j \in \mathcal{S}, j \neq i} ( X_{(k,i)}^{L} - X_{(k,j)}^{L} )$ 값이 크게 나올 것이다. 즉, $c$ 값이 작은 경우 planar feature($\mathcal{H}_k$)에 해당하고, 큰 경우 edge feature($\mathcal{E}_k$)에 해당한다.

논문에서는 1 sweep으로 얻은 데이터를 4개의 sub-region으로 나눈 후 각 sub-region에서 최대 2개의 edge points와 4개의 planar points를 사용하였다고 밝혔다. Edge points와 planar points는 $c$ 값이 특정 threshold보다 크거나 작을 경우에 해당한다.

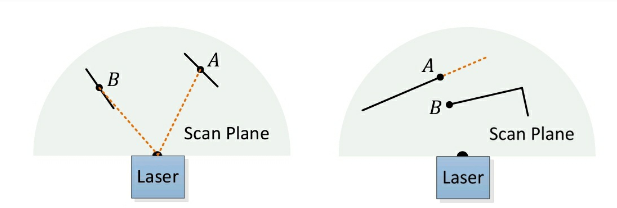outlier_case 출처: 원 논문

다음 상황과 같이 (a) local surface가 laser 방향과 거의 평행한 경우는 $c$를 계산할 때 정확도가 떨어진다. (b) 차폐로 인해 edge points로 오인된 경우 보는 각도에 따라 다른 feature로 인식될 수 있다. 따라서 두 경우를 outlier로 간주하여 제외한다.

[Note] 구현 상 오류(?)

implementation_error 출처: LeGO-LOAM Line by Line - 3. FeatureAssociation (1)

실제로 구현 코드에서는 valid pixel만을 사용하기 때문에 $X_{(k,j)}^{L} (j \in \mathcal{S})$가 일정한 간격의 horizontal한 점들로 구성되지 않을 수 있다는 오류가 있다고 한다. 그림과 같이 $X_{(k,i+5)}^{L}$가 다음 줄로 넘어가는 경우 엉뚱한 $c$ 값이 도출된다.

4.2 Finding Feature Point Correspondence

LiDAR odometry의 목적은

\[T_{k+1}^L = [ t_x, t_y, t_z, {\theta} _{x}, {\theta} _{y}, {\theta} _{z} ]\]

즉, $t_{k+1}$ 시점에서 로봇의 pose를 계산하는 것이다. 이때 $t$는 평행운동 성분, ${\theta}$는 회전운동 성분이다. 우선 sweep이 시작하기 전 $T_{k+1}^L$ 값을 초기화해준다. 논문에서는 $T_{k+1}^L = 0$으로 초기화하였으나, IMU가 있을 경우 IMU에서 측정한 속도 값으로 초기화할 수 있다.

로봇이 움직이면서 laser scan이 진행되므로 한 sweep에서 측정한 pointcloud이더라도 좌표계가 바뀔 수 있다. 따라서 점들을 기준 시점에서 측정했을 때의 좌표로 transform하는 작업이 필요한데, 이를 de-skewing이라고 한다.

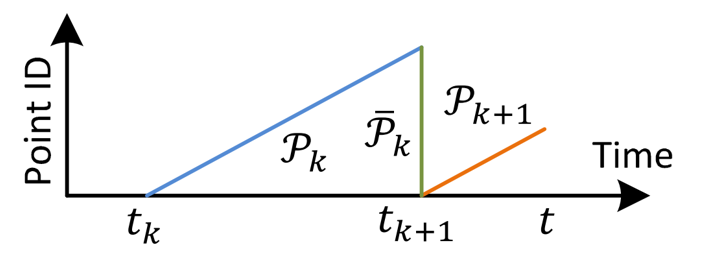time_diagram 출처: 원 논문

$t \in [t_{k+1}, t_{k+2}]$일 때, 즉 k+1번째 sweep을 수행중일 때를 보자. $P_{k}$는 완전히 갖고 있고, $P_{k+1}$은 그림과 같이 누적되고 있는 상태이다. 우리의 목표는 $t_{k+1}$ 시점에서 $P_{k}$와 $P_{k+1}$의 대응점을 탐색하는 것이다. 이를 위해서는 앞서 초기화한 $T_{k+1}^L$을 이용할 수 있다. 예를 들어 $P_{k} \rightarrow \bar{P_{k}}$로 transform할 때에는

\[\bar{ X}_{(k,i)}^L = R X_{(k,i)}^L + T_{(k+1,i)}^L [1:3] \Delta t\]

변환 공식을 이용한다. 이때 $\Delta t$는 특정 좌표의 점을 scan했을 때 시점과 기준 시점($t_{k+1}$)과의 차이고,

\[R = e^{\hat{\omega} \theta}\] \[\hat{\omega}= \textrm{Skew matrix of } \:\: T_{(k+1,i)}^L [4:6] \Delta t\] \[\theta = \textrm{Rotation angle}\]

로 정의된다. 마찬가지로 $P_{k+1}$에서 $t$까지 측정한 점들을 transform하여 $\tilde{P}_{k+1}$을 얻는다.

다음으로 edge feature, planar feature 각각에서 $\bar{P} _ {k}$, $\tilde{P} _ {k+1}$ 사이의 대응점을 탐색한다.

4.2.1 Edge feature

기본적인 아이디어는 외적을 이용하여 점과 직선 사이를 계산하는 것이다.

$i \in \tilde{\mathcal{E}}_{k+1}$인 edge point를 선택한다
$i$와 가깝고 연속적으로 위치한 $j, l \in \bar{P}_{k}$를 구한다.
Curvature $c$를 계산하여 $(j, l)$이 edge feature임이 확인된 경우

\[d_{\mathcal{E}}=\frac{|(\tilde{X}_{(k+1,i)}^L - \bar{X}_{(k,j)}^L)\times(\tilde{X}_{(k+1,i)}^L - \bar{X}_{(k,l)}^L)|}{|\bar{X}_{(k,j)}^L - \bar{X}_{(k,l)}^L|}\]

을 계산하여 edge feature에서의 거리 함수를 계산할 수 있다.

4.2.2 Planar feature

기본적인 아이디어는 외적을 이용하여 점과 평면 사이를 계산하는 것이다.

$i \in \tilde{\mathcal{H}}_{k+1}$인 edge point를 선택한다
$i$와 가깝고 연속적으로 위치한 $j, l, m \in \bar{P}_{k}$를 구한다.
Curvature $c$를 계산하여 $(j, l, m)$이 planar feature임이 확인된 경우

\[d_{\mathcal{H}}=\frac{ \begin{vmatrix} (\tilde{X}_{(k+1,i)}^L - \bar{X}_{(k,j)}^L) \\ (\bar{X}_{(k,j)}^L - \bar{X}_{(k,l)}^L)\times(\bar{X}_{(k,j)}^L - \bar{X}_{(k,m)}^L) \end{vmatrix}} {|(\bar{X}_{(k,j)}^L - \bar{X}_{(k,l)}^L)\times(\bar{X}_{(k,j)}^L - \bar{X}_{(k,m)}^L)|}\]

을 계산하여 planar feature에서의 거리 함수를 계산할 수 있다.

4.3 Motion Estimation

Edge, planar feature에서 도출한 거리 함수를 최소화하는 방향으로 $T_{k+1}^L$를 optimize해야 한다. 즉,

\[\textrm{Goal} : \underset{T_{k+1}^L}{\operatorname{argmin}} {\| \textbf{d}\|} \;\; \textrm{where} \;\; \textbf{d} = \begin{bmatrix} d_{\mathcal{E}} \\ d_{\mathcal{H}} \end{bmatrix} = \begin{bmatrix} f_{\mathcal{E}}(X_{(k+1,i)}^L, T_{k+1}^L) \\ f_{\mathcal{H}}(X_{(k+1,i)}^L, T_{k+1}^L) \end{bmatrix}\]

로 정리할 수 있다. 본 논문에서는 Levenberg-Marquardt 알고리즘을 사용하여 optimization을 수행한다고 밝혔다.

\[T_{k+1}^L \leftarrow T_{k+1}^L - (J^{T}J + \lambda \cdot \textrm{diag}(J^{T}J))^{-1} J^{T} \textbf{d}(T_{k+1}^L)\]

이를 위해서는 $\textbf{d}$의 Jacobian matrix가 필요하다. 구현 코드를 보면 직접 수식을 전개하여 계산한 것으로 보인다.

[Note] Levenberg-Marquardt method
Gradient descent method와 Gauss-Newton method을 결합한 방법이다. 해에서 멀리 떨어져 있을 때에는 Gradient descent method가 우세하여 빠르게 해에 수렴하고, 해 근처에 있을 때에는 Gauss-Newton method가 우세하게 작동한다. Gauss-Newton method보다 안정적으로 해를 탐색할 수 있고, 빠르게 해에 수렴한다는 장점이 있다.

Gradient descent method

\[x_{k+1} = x_{k} - \alpha J^{T} f(x_{k})\]

Gauss-Newton method

\[x_{k+1} = x_{k} - \textrm{pinv}(J) f(x_{k}) = x_{k} - (J^{T}J)^{-1}J^{T} f(x_{k})\]

Levenberg-Marquardt method

\[x_{k+1} = x_{k} - (J^{T}J + \alpha \cdot \textrm{diag}(J^{T}J))^{-1} J^{T} f(x_{k})\]

5. LiDAR Mapping

LiDAR Odometry와 달리 LiDAR Mapping은 sweep이 마무리될 때마다 수행된다. LiDAR Odometry 단계에서 계산한 de-skewing된 $\bar{P} _ {k+1}$를 $\{W\}$에 registration한다.

$k$번째 sweep이 끝난 후 world map에 registration된 pointcloud를 $Q_{k}$이라 하고, $T_{k+1}^{W}$에 의해 transform된 $\bar{P} _ {k+1}$를 $\bar{Q} _ {k+1}$라고 하자. 이때 우리의 목표는 LiDAR Odometry 과정과 유사하게 $T_{k+1}^{W}$를 최적화하여 적절한 $\bar{Q}_{k+1}$를 구하는 것이다.

LiDAR Odometry 단계와 마찬가지로 feature extraction, finding feature point correspondence, motion estimation 과정을 거쳐 $\bar{Q}_{k+1}$를 계산한다. 몇 가지 차이점은 아래에 정리하였다.

LiDAR Mapping은 LiDAR Odometry보다 더 작은 주기로 수행되므로(10Hz vs 1Hz) 10배 많은 point를 사용한다. 따라서 10배 많은 edge, planar feature를 사용한다.
Edge, planar feature를 판별할 때 feature point 주변의 point $\mathcal{S’}$에 대하여 eigen decomposition을 수행한다. 3개의 eigenvalue ${\lambda} _ {1} > {\lambda} _ {2} > {\lambda} _ {3}$에 대해

\[{\lambda} _ {1} \gg {\lambda} _ {2} > {\lambda} _ {3}\]

이면 edge feature,

\[{\lambda} _ {1} > {\lambda} _ {2} \gg {\lambda} _ {3}\]

이면 planar feature로 분류한다.

6. Transform Integration

최종적으로 LiDAR의 pose는 sweep 당 1번씩(1Hz) $T_{k+1}^{W}$을 사용하여 update하고, 10Hz마다 $T_{k+1}^{L}$을 사용하여 update한다.