SO(3) group에 이어서 SE(3) group에 대해 정리해본다.
관련 포스팅
reference textbook
Lynch, Kevin M., and Frank C. Park. Modern robotics. Cambridge University Press, 2017.
1. Special Euclidean Group, SE(3)
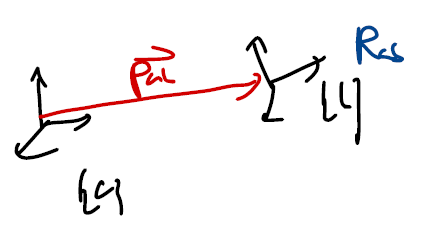
$SE(3)$ group은 강체의 3차원 상 운동을 기술한다. 강체의 운동은 크게 회전 운동과 병진(평행) 운동으로 나눌 수 있다는 점에 착안하면, 회전 운동은 $SO(3)$ matrix $R$으로, 평행 이동은 3차원 벡터 $p \in \mathbb{R}^3$로 표현할 수 있다. 이를 종합하여 $T \in SE(3)$은 $4 \times 4$ matrix로 다음과 같이 표현된다.
\[T = \begin{bmatrix} R & p \\ 0 & 1\end{bmatrix} =\begin{bmatrix} r_{11} & r_{12} & r_{13} & p_1\\ r_{21} & r_{22} & r_{23} & p_2\\ r_{31} & r_{32} & r_{33} & p_3\\ 0 & 0 & 0 & 1\end{bmatrix}\]이때 $p$는 변환 전 좌표계에서 기술한 병진 운동 성분이라는 점에 유의하여야 한다. $R$에 의해 회전된 좌표계에서 기술한 방향이 아니다.
2. SE(3) 성질
SE(3) 행렬이 만족하는 성질을 정리하면 다음과 같다.
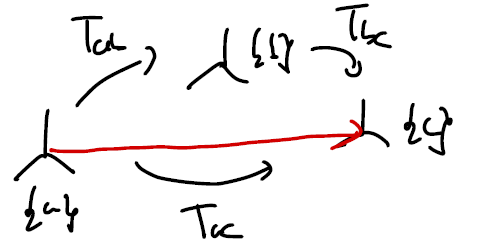
- {a} $\rightarrow$ {b} 좌표계로 변환하고 {b} $\rightarrow$ {c} 좌표계로 변환한 결과는 {a} $\rightarrow$ {c} 좌표계로 변환한 결과와 동일하다.
- 항상 역변환이 존재하므로, 역행렬이 존재한다.
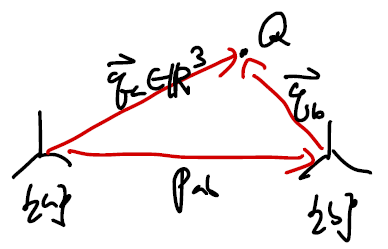
- 공간 상의 점 $Q$를 {a} 좌표계, {b} 좌표계에서 기술한 위치 벡터를 $q_a, q_b$라 할 때,
(이때 차원을 맞추기 위하여 $q_a = \begin{bmatrix} q_x & q_y & q_z & 1\end{bmatrix}^T$로 정의한다.)
3. Screw motion and SE(3)
Chasles’ - Mozzi theorem에 의하면 모든 강체 운동은 그에 대응하는 나선 운동(Screw motion) 이 존재한다. 따라서 임의의 $T \in SE(3)$은 그에 대응하는 나선 운동을 찾을 수 있다.
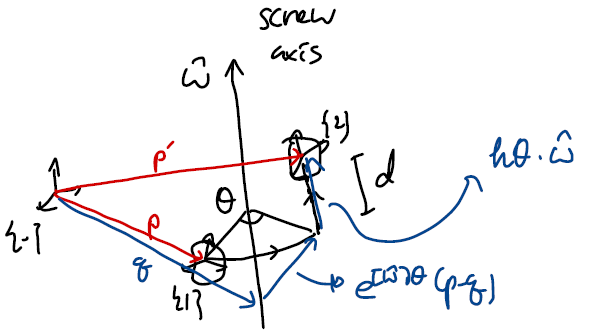
$T_{01} = \begin{bmatrix} R & p \\ 0 & 1\end{bmatrix}, \;\; T_{02} = \begin{bmatrix} R’ & p’ \\ 0 & 1\end{bmatrix}$라 두자. $T_{02}$는 그림에서 파란색으로 표시한 3개의 화살표를 통해서도 계산할 수 있다.
- 첫번째 화살표 : 임의의 회전축 위의 한 점을 향하는 벡터 $q$
- 두번째 화살표 : screw axis $\hat{\omega}$를 기준으로 $(p-q)$를 $\theta$만큼 회전시켰으므로 $(p-q)e^{[\hat{\omega}]\theta}$
- 세번째 화살표 : screw axis 방향으로 $d$만큼 이동하므로 $d\hat{\omega} = h \theta \hat{\omega}$ (이때 $h$는 pitch of screw, i.e. $h = \frac{d}{\theta}$)
따라서
\[p' = q + (p-q)e^{[\hat{\omega}]\theta} + h \theta \hat{\omega}\]로 나타낼 수 있다. 회전행렬의 경우 screw axis를 기준으로 회전시킨 경우만 고려하면 되므로,
\[R' = e^{[\hat{\omega}]\theta}\]이다. 이 둘을 종합하면
\[\begin{bmatrix} R' & p' \\ 0 & 1\end{bmatrix} = \begin{bmatrix} e^{[\hat{\omega}]\theta} & (I - e^{[\hat{\omega}]\theta})q + h \theta \hat{\omega} \\ 0 & 1\end{bmatrix} \begin{bmatrix} R & p \\ 0 & 1\end{bmatrix}\]이 성립한다.
5. Exponential Coordinate of SE(3)
$SO(3)$ group에서 $R = e^{[\hat{\omega}]\theta}$와 같이 exponential form으로 표현한 것 처럼 $T \in SE(3)$ 역시 $e^{[\mathcal{S}]\theta}$와 같은 exponential form으로 나타낼 수 있다. 이때
\[\mathcal{S} = \begin{bmatrix} \hat{\omega} \\ v\end{bmatrix} \in \mathbb{R}^6, \;\; [\mathcal{S}] = \begin{bmatrix} [\hat{\omega}] & v \\ 0 & 0\end{bmatrix} \in se(3)\]로 표현한다. 주의할 점은 $se(3)$에 속하는 $4 \times 4$ matrix는 4행 4열 성분이 0이라는 점이다. $SE(3)$에 속하는 matrix는 4행 4열 성분이 1이었다는 점을 상기하자.
위 식에서 $\hat{\omega}$는 screw axis 단위 방향 벡터이다. Tayler expansion을 이용하여 식을 변형하면 다음과 같다.
\[\begin{align*} \begin{bmatrix} e^{[\hat{\omega}]\theta} & (I - e^{[\hat{\omega}]\theta})q + h \theta \hat{\omega} \\ 0 & 1\end{bmatrix} &= e^{[\mathcal{S}]\theta} = I + [\mathcal{S}]\theta + \frac{1}{2!} [\mathcal{S}]^2 \theta^2 + \cdots \\ &= I + \begin{bmatrix} [\hat{\omega}] & v \\ 0 & 0\end{bmatrix} \theta + \frac{1}{2!} \begin{bmatrix} [\hat{\omega}] & v \\ 0 & 0\end{bmatrix}^2 \theta^2 + \frac{1}{3!}\begin{bmatrix} [\hat{\omega}] & v \\ 0 & 0\end{bmatrix}^3 \theta^3 + \cdots \\ &= I + \begin{bmatrix} [\hat{\omega}] & v \\ 0 & 0\end{bmatrix} \theta + \frac{1}{2!} \begin{bmatrix} [\hat{\omega}]^2 & [\hat{\omega}]v \\ 0 & 0\end{bmatrix} \theta^2 + \frac{1}{3!}\begin{bmatrix} -[\hat{\omega}] & [\hat{\omega}]^2 v \\ 0 & 0\end{bmatrix} \theta^3 + \cdots \\ &= \begin{bmatrix} e^{[\hat{\omega}]\theta} & G(\theta)v \\ 0 & 1\end{bmatrix} \end{align*}\]이때 $[\hat{\omega}]^3 = - [\hat{\omega}]$라는 사실을 이용하였다. $G(\theta)$는 4열 성분을 분석하면 다음과 같이 계산할 수 있다.
\[\begin{align*} G(\theta)v &= 0 + v\theta + \frac{1}{2!}[\hat{\omega}]v \theta^2 + \frac{1}{3!}[\hat{\omega}]^2 v \theta^3 + \cdots\\ &=\left( I \theta + \frac{1}{2!}[\hat{\omega}] \theta^2 + \frac{1}{3!}[\hat{\omega}]^2 \theta^3 + \cdots \right)v \\ &=\left( I \theta + [\hat{\omega}] \left(\frac{1}{2!}\theta^2 - \frac{1}{4!}\theta^4 + \cdots \right) + [\hat{\omega}]^2 \left(\frac{1}{3!}\theta^3 - \frac{1}{5!}\theta^5 + \cdots \right)\right)v \\ &=\left( I \theta + (1-\cos{\theta})[\hat{\omega}] + (\theta - \sin{\theta})[\hat{\omega}]^2 \right)v \end{align*}\] \[\therefore G(\theta) = \left( I \theta + (1-\cos{\theta})[\hat{\omega}] + (\theta - \sin{\theta})[\hat{\omega}]^2 \right)\] \[(I - e^{[\hat{\omega}]\theta})q + h \theta \hat{\omega} = \left( I \theta + (1-\cos{\theta})[\hat{\omega}] + (\theta - \sin{\theta})[\hat{\omega}]^2 \right)v\]또한 $v$는 다음과 같다. 유도하지는 않지만, 대입을 통해 확인만 해보도록 한다.
\[v = -\hat{\omega} \times q + h\hat{\omega} = -[\hat{\omega}]q + h\hat{\omega}\]Check
\[\left( I \theta + (1-\cos{\theta})[\hat{\omega}] + (\theta - \sin{\theta})[\hat{\omega}]^2 \right) \left( -[\hat{\omega}]q + h\hat{\omega} \right)\] \[\begin{align*} &=-[\hat{\omega}]\theta q + h \theta \hat{\omega} - \left(1-\cos{\theta}\right)[\hat{\omega}]^2 q + \left(\theta - \sin{\theta}\right)[\hat{\omega}]q \\ &=\left(-\sin{\theta}[\hat{\omega}] - (1-\cos{\theta})[\hat{\omega}]^2\right)q + h \theta \hat{\omega} \\ &= (I - e^{[\hat{\omega}]\theta})q + h \theta \hat{\omega} \end{align*}\]식 전개 과정에서 $[\hat{\omega}]\hat{\omega} = \hat{\omega} \times \hat{\omega} = 0$이 사용되었다. 또한 $e^{[\hat{\omega}]\theta} = I + \sin{\theta} [\hat{\omega}] + (1 - \cos{\theta}) [\hat{\omega}]^2$을 적용하였다.
$SO(3)$과 마찬가지로 matrix logarithm을 정의할 수 있다. 그 알고리즘은 아래와 같다.
- $R = I \; : \; \hat{\omega} = 0, \; v = \frac{p}{|p|}, \; \theta = |p|$
- $\textrm{Otherwise}, \;\; \hat{\omega}\theta = \log{R}, \;v = G^{-1} (\theta)p, \;\; \textrm{where}$
4. Twist or Spacial velocity
$SO(3)$에서 $[\omega_s] = \dot{R} R^{-1}$, $[\omega_b] = R^{-1} \dot{R}$이 성립하였던 것처럼, $SE(3)$에서도 유사한 관계가 존재한다.
\[\begin{align*} \dot{T} T^{-1} &= \begin{bmatrix} \dot{R} & \dot{p} \\ 0 & 0\end{bmatrix} \begin{bmatrix} R^T & -R^T p \\ 0 & 1\end{bmatrix} \\ &= \begin{bmatrix} \dot{R} R^T & -\dot{R} R^T p + \dot{p} \\ 0 & 0\end{bmatrix} \\ &= \begin{bmatrix} [\omega _ s] & \dot{p} - [\omega _ s]p \\ 0 & 0\end{bmatrix} =: \begin{bmatrix} [\omega _ s] & v_s \\ 0 & 0\end{bmatrix} \in se(3) \end{align*}\]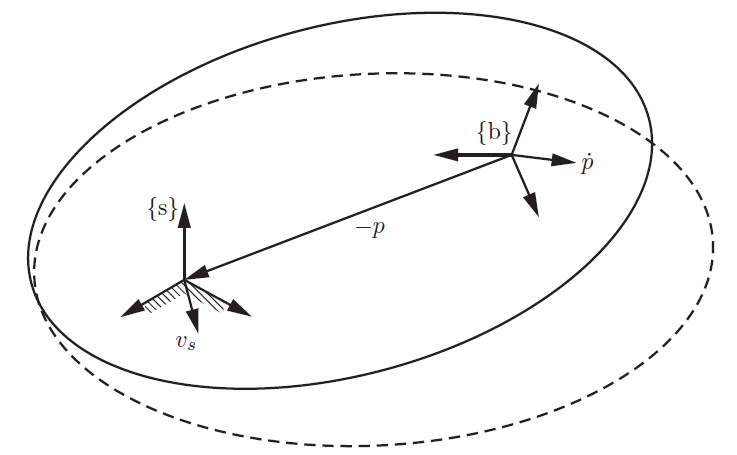
$\dot{T} T^{-1}$의 계산 결과를 분석해보자. $[\omega _ s]$는 각속도의 skew-symmetric form을 space coordinate에서 표현한 값이다. $[\omega _ s]p = \omega _ s \times p$인 점에 착안하면 $\dot{p} - [\omega _ s]p$는 {s} frame의 원점에 해당하는 강체 상 한점이 움직이는 선속도를 space coordinate에서 나타낸 값이다. 자세한 내용은 그림을 참고하자.
즉, $\dot{T} T^{-1}=:[\mathcal{V}_s]$는 {s} frame에서 표현한 {s} frame의 원점의 각속도와 선속도를 의미한다. Skrew motion으로 해석하였던 강체의 운동은 실재적인 물리적 의미를 갖는다. 따라서 $[\mathcal{V}_s]$를 spatial velocity in space frame 또는 space twist라고 정의한다.
\[\begin{align*} T^{-1} \dot{T} &= \begin{bmatrix} R^T & -R^T p \\ 0 & 1\end{bmatrix} \begin{bmatrix} \dot{R} & \dot{p} \\ 0 & 0\end{bmatrix} \\ &= \begin{bmatrix} R^T \dot{R} & R^T\dot{p} \\ 0 & 0\end{bmatrix} =: \begin{bmatrix} [\omega _ b] & v_b \\ 0 & 0\end{bmatrix} \in se(3) \end{align*}\]마찬가지로 $T^{-1} \dot{T}$를 계산해보면 $[\omega _ b]$는 {b} frame에서 나타낸 강체의 각속도를 의미하고, $v_b = R^T \dot{p}$는 {b} frame에서 나타낸 {b} frame의 원점의 선속도를 의미한다. 따라서 $[\mathcal{V}_b] := T^{-1} \dot{T}$를 spatial velocity in body frame 또는 body twist라고 정의한다.
$[\mathcal{V}_s]=\dot{T} T^{-1}, \;\; [\mathcal{V}_b] = T^{-1} \dot{T}$에서
\[\begin{align*} [\mathcal{V}_s] &= T [\mathcal{V}_b] T^{-1} \\ &= \begin{bmatrix} R & p \\ 0 & 1\end{bmatrix} \begin{bmatrix} [\omega _ b] & v_b \\ 0 & 0\end{bmatrix} \begin{bmatrix} R^T & -R^T p \\ 0 & 1\end{bmatrix} \\ &= \begin{bmatrix} R [\omega _ b] R^T & - R [\omega _ b] R^T p + R v_b \\ 0 & 0\end{bmatrix} \\ &= \begin{bmatrix} [R \omega _ b] & [p]R \omega _ b + R v_b \\ 0 & 0\end{bmatrix} \end{align*}\] \[\therefore \omega _ s = R \omega _b , \;\;\; v_s = [p]R \omega _ b + R v_b\] \[\mathcal{V}_s = \begin{bmatrix} \omega _ s \\ v_s \end{bmatrix} = \begin{bmatrix} R & 0 \\ [p]R & R\end{bmatrix} \begin{bmatrix} \omega _ b \\ v_b \end{bmatrix} = \begin{bmatrix} R & 0 \\ [p]R & R\end{bmatrix} \mathcal{V}_b\]와 같은 변환 관계가 성립한다. 이처럼 두 spatial velocitys(twists)는 $6 \times 6$ matrix인 adjoint representation을 통해 변환된다.
\[[\textrm{Ad}_T] := \begin{bmatrix} R & 0 \\ [p]R & R\end{bmatrix}\] \[\mathcal{V}' = [\textrm{Ad}_T] \mathcal{V} \;\; \textrm{or} \;\; [\mathcal{V}'] = \textrm{Ad}_T(\mathcal{V})\]