[Lie group] SO(3) group 정리

LIO-SAM 논문 리딩을 위해 IMU preintegration에 대해 공부하다 보니 Lie group에 대한 깊은 이해가 필요하다는 것을 느꼈다. 3학년 1학기 때 “로봇 공학 입문” 수업을 들으며 Lie group에 대해 공부했었는데, 향후 논문 리딩에 많이 참고할 것 같아 따로 정리해 두려고 한다. 아래 등장하는 그림들은 수업 시간에 필기한 자료를 가져왔음을 미리 밝혀둔다.

reference textbook
Lynch, Kevin M., and Frank C. Park. Modern robotics. Cambridge University Press, 2017.

1. Special Orthogonal Group, SO(3)

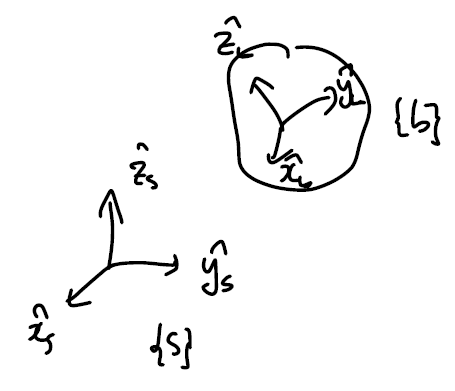
그림은 space frame(s)에서 바라본 body frame(b)를 나타내었다. 이때 두 좌표계의 기저 벡터 사이 관계는 다음과 같은 $3\times 3$ matrix로 기술할 수 있을 것이다.

$$\left[\begin{array}{c}{\hat{x}}_b\\ {\hat{y}}_b\\ {\hat{z}}_b\end{array}\right]=\left[\begin{array}{ccc}{r}_{11}& r_{12}& r_{13}\\ r_{21}& r_{22}& r_{23}\\ r_{31}& r_{32}& r_{33}\end{array}\right]\left[\begin{array}{c}{\hat{x}}_s\\ {\hat{y}}_s\\ {\hat{z}}_s\end{array}\right]$$

이때 $R=[r_{ij}]$가 만족해야 할 조건은 다음과 같다.

• Unit vector : $|{\hat{x}}_b|=|{\hat{y}}_b|=|{\hat{z}}_b|=1$ i.e. $\sum _{i=1}^3{r}_{ij}^2=1(j=1,2,3)$
• Orthogonality : ${\hat{x}}_b\cdot {\hat{y}}_b={\hat{y}}_b\cdot {\hat{z}}_b={\hat{z}}_b\cdot {\hat{x}}_b=0$
• Right-hand coordinate : $detR=1$

이러한 3개의 조건을 만족하는 $3\times 3$ matrix은 3차원 상의 회전을 기술한다. 이들의 집합을 SO(3)이라고 한다. 한편 위 상황과 같이 {s}에서 바라본 {b}의 rotation을 $R_{sb}$로 나타낸다.

2. SO(3) 성질

SO(3) 행렬이 만족하는 성질을 정리하면 다음과 같다.

• $R{R}^T=R^{T}R=I$
• $R^T=R^{-1}$

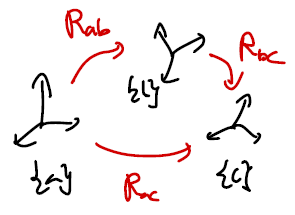
• $R_1,R_2\in SO(3)\Rightarrow R_1{R}_2\in SO(3)$
• 특히, $R_{ab},R_{bc}\in SO(3)\Rightarrow R_{ab}{R}_{bc}=R_{ac}\in SO(3)$

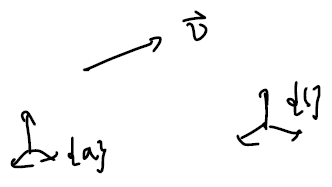
• 동일한 벡터 $\overrightarrow{v}$를 서로 다른 두 좌표계 {a}, {b}에서 기술할 때, $\overrightarrow{v_a}=R_{ab}\overrightarrow{v_b}$

3. Angular velocity and skew-symmetric matrix

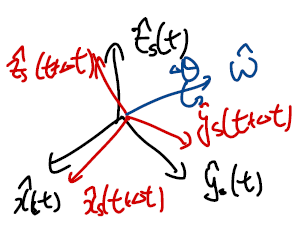
그림과 같이 각속도 벡터 $\omega =\dot{\theta }\hat{\omega }$에 의해 좌표계가 회전하는 상황을 고려하자. 이때 단위벡터 $\hat{x}$가 시간에 따라 변화하는 방향 변화율은

$$\dot{\hat{x}}=\omega \times \hat{x}$$

로 기술할 수 있다. 이는 $\hat{y},\hat{z}$에 대해서도 마찬가지이다.

이 식에 ${\left[\begin{array}{ccc}{\hat{x}}_b& {\hat{y}}_b& {\hat{z}}_b\end{array}\right]}^T=R{\left[\begin{array}{ccc}{\hat{x}}_s& {\hat{y}}_s& {\hat{z}}_s\end{array}\right]}^T$을 대입했다고 생각하면 $R$의 각 열벡터 $r_i(i=1,2,3)$는 다음이 성립한다.

$$\dot{r_i}={\omega }_s\times r_i$$

열벡터를 종합하면 시간에 따른 $SO(3)$ matrix $R$의 변화율 $\dot{R}(t)$를 다음과 같이 기술할 수 있다.

$$\dot{R}=\left[\begin{array}{ccc}{\omega }_s\times r_1& {\omega }_s\times r_2& {\omega }_s\times r_3\end{array}\right]=[{\omega }_s]R$$

이때 $[{\omega }_s]$ skew-symmetric(i.e. $[{\omega }_s{]}^T=-[{\omega }_s]$)을 만족하는 행렬이다. 이러한 skew-symmetric matrix를 모아둔 집합을 $so(3)$이라고 한다.

$$[\omega ]=\left[\begin{array}{ccc}0& -{\omega }_3& -{\omega }_2\\ {\omega }_3& 0& -{\omega }_1\\ -{\omega }_2& {\omega }_1& 0\end{array}\right]$$

몇가지 성질을 아래에 정리해 두었다.

• $R\in SO(3),R[\omega ]R^T=[R\omega ]$
• $\dot{R}=[{\omega }_s]R$으로부터, $[{\omega }_s]=\dot{R}{R}^{-1}=\dot{R}{R}^T$
• ${\omega }_b$를 body frame에서 기술한 각속도 벡터라고 할 때,

$$[{\omega }_b]=[R^T{\omega }_s]=R^T[{\omega }_s]R=R^T(\dot{R}{R}^{-1})R=R^{-1}\dot{R}$$

4. Exponential Coordinate of SO(3)

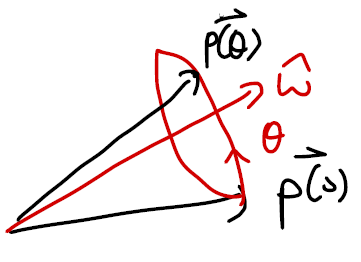
벡터 $p$가 크기가 1인 unit angular velocity 벡터 $\hat{\omega }$를 따라 회전할 때 $p$의 속도 $\dot{p}$는

$$\dot{p}=\hat{\omega }\times p=[\hat{\omega }]p$$

이다. 이는 matrix differential equation form이고, 초기조건 $p(0)$이 주어졌을 때 해는

$$p(t)=e^{[\hat{\omega }]t}p(0)$$ $$p(\theta )=e^{[\hat{\omega }]\theta }p(0)$$

이다. 특히 exponential part를 tayler expansion하면

$$e^{[\hat{\omega }]\theta }=I+[\hat{\omega }]\theta +[\hat{\omega }{]}^2\frac{{\theta }^2}{2}+\cdots$$

이 성립한다.

[Remark] Cayley-Hamilton theorem
행렬 A의 특성다항식

$$P(s)=det(sI-A)=s^n+a_{n-1}{s}^{n-1}+\cdots +a_0$$

에 대하여 다음 식이 성립한다.

$$P(A)=A^n+a_{n-1}{A}^{n-1}+\cdots +a_0=O$$

$|\hat{\omega }|=1$에 유의하여 $[\hat{\omega }]$의 특성다항식을 계산하면

$$P(s)=s^3+s$$

이므로

$$P([\hat{\omega }])=[\hat{\omega }{]}^3+[\hat{\omega }]=O$$

가 성립한다. 이를 이용하면 exponential part는

$$\begin{array}{rl}{e}^{[\hat{\omega }]\theta }& =I+[\hat{\omega }]\theta +[\hat{\omega }{]}^2\frac{{\theta }^2}{2!}+[\hat{\omega }{]}^3\frac{{\theta }^3}{3!}+\cdots \\ & =I+[\hat{\omega }]\theta +[\hat{\omega }{]}^2\frac{{\theta }^2}{2!}-[\hat{\omega }]\frac{{\theta }^3}{3!}+\cdots \\ & =I+(\theta -\frac{{\theta }^3}{3!}+\cdots )[\hat{\omega }]+(\frac{{\theta }^2}{2!}-\frac{{\theta }^4}{4!}+\cdots )[\hat{\omega }{]}^2\\ & =I+\sin \theta [\hat{\omega }]+(1-\cos \theta )[\hat{\omega }{]}^2\end{array}$$

와 같이 정리된다. 따라서 3차원 상에서 회전축 $\hat{\omega }$와 각도 $\theta$를 알 때 $SO(3)$ 행렬 $R$을

$$R=e^{[\hat{\omega }]\theta }=I+\sin \theta [\hat{\omega }]+(1-\cos \theta )[\hat{\omega }{]}^2$$

로 나타낼 수 있는데 이를 Rodrigues’ rotation formula라고 한다.

$[\hat{\omega }]\theta \in so(3)$에서 $R\in SO(3)$으로 가는 변환을 matrix exponential로 나타낼 수 있으므로 그 역변환인 matrix logarithm을 생각할 수 있다. 이는 다음과 같은 알고리즘으로 계산 가능하다.

1. $R=I:\theta =0,\hat{\omega }:\text{undefined}$
2. $\text{tr}(R)=-1:\theta =\pi ,\text{solve}R=I+2[\hat{\omega }{]}^2$
3. $\text{Otherwise},\cos \theta =\frac{1}{2}(\text{tr}(R)-1),[\hat{\omega }]=\frac{1}{2\sin \theta }(R-R^T)$